
AI 분야에서 수학적 추론은 항상 사랑과 증오의 문제였습니다. 왜? 추상적인 개념을 이해하는 것뿐만 아니라, 정확하고 여러 단계에 걸친 논리적 추론도 필요하기 때문입니다.
이전 언어 모델은 유창하게 텍스트를 생성할 수 있었지만, 복잡한 수학 문제에 직면했을 때 어디서부터 시작해야 할지 모르는 경우가 많았습니다.
마치 인문학도에게 올림피아드 수학 문제를 풀라고 하는 것과 같았습니다. 하지만 NVIDIA가 최근 출시한 OpenMath-Nemotron 시리즈 모델은 이 문제를 직접적으로 해결합니다! 오늘은 이 강력한 새로운 AI 스타에 대해 이야기해 보겠습니다.
왜 수학적 추론이 그렇게 어려울까?
AI 분야에서 수학적 추론은 산과 같습니다. AI는 수학적 개념을 이해할 뿐만 아니라 인간처럼 논리적 추론을 수행할 수 있어야 합니다. 예를 들어, 복잡한 기하 문제를 풀려면 공식을 기억해야 할 뿐만 아니라, 공식을 단계별로 유도하는 방법도 알아야 합니다. 기존 언어 모델은 매우 유창한 텍스트를 생성할 수 있지만, 심층적인 논리를 요구하는 수학 문제에는 대처할 수 없습니다. 이는 마치 수필을 잘 쓰는 사람에게 복잡한 수학 문제를 풀라고 요구하는 것과 같습니다. 얼마나 어려운지 상상할 수 있을 거예요.
엔비디아의 새로운 무기: OpenMath-Nemotron 시리즈
이번에 엔비디아가 출시한 OpenMath-Nemotron 시리즈 모델은 특별히 수학적 추론에 맞춰 제작되었다고 할 수 있습니다. 이 시리즈에는 OpenMath-Nemotron-32B와 OpenMath-Nemotron-14B-Kaggle의 두 가지 버전이 포함됩니다. 이러한 모델은 모두 대규모 미세 조정을 통해 학습되고 수학 문제에 맞게 특별히 최적화된 Qwen 계열의 Transformer 모델을 기반으로 합니다.
OpenMath-Nemotron-32B: 플래그십 버전의 힘
OpenMath-Nemotron-32B는 이 시리즈의 주력 버전으로, 328억 개의 매개변수와 BF16 텐서 연산을 사용하고 하드웨어 활용 효율성이 매우 높습니다. OpenMathReasoning 데이터 세트에서 Qwen2.5-32B를 미세 조정하여 학습했습니다. 이 데이터 세트에는 수학 경시대회와 표준화된 시험에서 나온 난이도 높은 문제가 포함되어 있으며, 수학적 추론을 위해 맞춤 제작되었다고 할 수 있습니다.
이 모델은 여러 가지 엄격한 벤치마크에서 최첨단 결과를 달성했습니다. 예를 들어, 2024년과 2025년 미국 초대 수학 경시대회(AIME)와 하버드-MIT 수학 경시대회(HMMT)에서 이전 상위 모델보다 우수한 성적을 거두었습니다. Tool Integrated Reasoning(TIR) 모드에서는 AIME24에서 평균 합격률 78.4%, 다수결 투표 정확도 93.3%를 달성했습니다.
다양한 요구 사항을 충족하는 3가지 추론 모드
이 모델을 다양한 추론 시나리오에 적용하기 위해 OpenMath-Nemotron-32B는 세 가지 모드, 즉 사고의 사슬(CoT), 도구 통합 추론(TIR), 생성적 솔루션 선택(GenSelect)을 지원합니다.
- 사고의 사슬(CoT) 모델 : 이 모델은 최종 답변을 제공하기 전에 중간 추론 단계를 생성합니다. AIME24에서는 합격률이 76.5%입니다.
- 생성적 솔루션 선택(GenSelect) 모드 : 이 모드는 여러 후보 솔루션을 생성한 다음 가장 일관된 답을 선택합니다. AIME24에서는 놀랍게도 93.3%의 정확도를 달성했습니다.
이 세 가지 모드를 사용하면 사용자는 투명성이 요구되는 연구 환경이든 속도와 안정성이 요구되는 프로덕션 환경이든 필요에 따라 설명의 풍부함과 답변의 정확성 사이의 균형을 맞출 수 있습니다.
OpenMath-Nemotron-14B-Kaggle: 작지만 강력한 경쟁 도구
NVIDIA는 32B 버전 외에도 경쟁 시나리오에 특별히 최적화된 148억 개의 매개변수를 갖춘 모델인 OpenMath-Nemotron-14B-Kaggle을 출시했습니다.
이 제품은 고급 수학 문제를 푸는 데 중점을 둔 AIMO-2 Kaggle 경연대회에서 1위를 차지했습니다. 경쟁의 형식과 난이도에 더 잘 맞도록 훈련 데이터를 조정함으로써, 이 모델은 높은 적응성을 보여주었습니다.
AIME24에서 CoT 모드에서 14B-Kaggle 모델의 통과율은 73.7%에 도달했고, GenSelect 모드에서는 86.7%로 증가했습니다. AIME25에서는 57.9%의 합격률(과반수 득표율 64.3%)을 달성했고, HMMT-24-25에서는 50.5%의 합격률(과반수 득표율 64.8%)을 달성했습니다.
이러한 데이터는 매개변수가 적더라도 이 모델이 여전히 고품질 솔루션을 제공할 수 있으며 리소스가 제한적이거나 낮은 지연 시간이 필요한 시나리오에 매우 적합하다는 것을 보여줍니다.
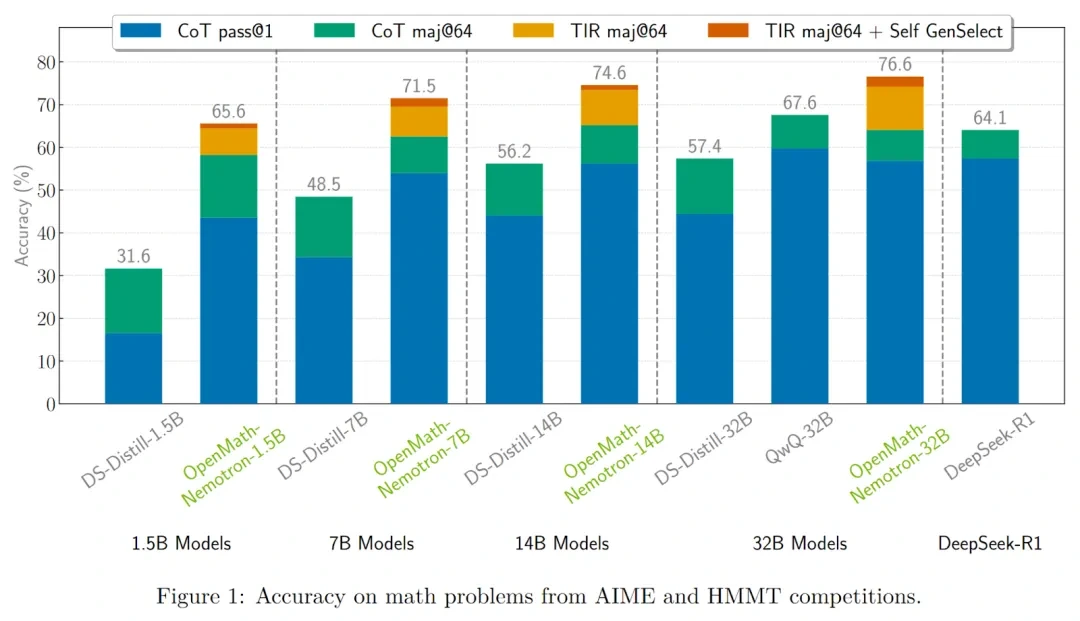
오픈소스 파이프라인으로 개발이 더 쉬워집니다
NVIDIA는 데이터 생성, 교육 프로세스, 평가 프로토콜을 포함하여 두 모델 모두에 대한 완전한 오픈 소스 파이프라인을 제공합니다.
이러한 워크플로는 NVIDIA의 NeMo-Skills 프레임워크에 통합되어 CoT, TIR 및 GenSelect 추론 모드의 참조 구현을 제공합니다. 개발자는 샘플 코드를 통해 신속하게 Transformer 파이프라인을 구축하고, 데이터 유형과 장치 매핑을 구성하고, 모델 출력을 구문 분석하여 이러한 모델을 쿼리하는 애플리케이션을 신속하게 개발할 수 있습니다.
효율적인 하드웨어 최적화
두 모델 모두 Ampere에서 Hopper 마이크로아키텍처에 이르는 NVIDIA의 GPU 아키텍처에서 효율적으로 실행되도록 최적화되어 있으며, 고도로 최적화된 CUDA 라이브러리와 TensorRT 최적화를 활용합니다.
실제 운영에 배포하는 경우 사용자는 Triton Inference Server를 통해 저지연, 고처리량 통합을 달성할 수 있으며, 이를 통해 네트워크 서비스와 일괄 처리 프로세스를 쉽게 처리할 수 있습니다.
BF16 텐서 포맷을 채택하면 수치적 정확도와 메모리 사용량의 균형을 이룰 수 있어 다양한 하드웨어 플랫폼에서 강력한 성능을 유지하면서도 대규모 모델을 GPU 메모리 제한 내에서 실행할 수 있습니다.
미래 전망: 수학적 추론의 새로운 방향
NVIDIA의 OpenMath-Nemotron 모델군은 현재의 수학적 추론 작업에서 탁월한 성과를 보일 뿐만 아니라, 향후 개발 방향을 제시합니다. 앞으로 이러한 모델은 더욱 진보된 대학 수학으로 확장되어 다중 모드 입력(예: 손으로 쓴 방정식)을 지원하고, 생성된 솔루션을 검증하고 향상시키기 위해 기호 계산 엔진과 더욱 긴밀하게 통합될 수 있습니다.
요약: 수학적 추론의 새로운 시대
NVIDIA의 OpenMath-Nemotron 모델 시리즈는 수학적 추론을 위한 특별한 미세 조정을 통해 수학적 추론에서 언어 모델의 단점을 성공적으로 해결합니다. 32B 매개변수 버전은 여러 벤치마크에서 최고의 결과를 달성했으며 설명의 풍부함과 답변의 정확성을 균형 있게 조절하기 위해 세 가지 추론 모드를 제공했습니다.
14B-Kaggle 버전은 경쟁 시나리오에서 좋은 성과를 보였으며, 더 작은 매개변수 규모에서도 높은 효율성을 보였습니다. 두 모델 모두 오픈 소스 파이프라인을 통해 완벽하게 재현 가능하며, 모든 추론 모드의 참조 구현은 NVIDIA의 NeMo-Skills 프레임워크를 통해 제공됩니다. 하드웨어에 최적화되어 있을 뿐만 아니라, 미래의 고급 수학 응용 프로그램을 위한 기반도 마련합니다.
AI 지원 교육 시스템이든, 학업 경쟁 준비 도구이든, 형식적 또는 상징적 추론이 필요한 과학적 컴퓨팅 워크플로이든, OpenMath-Nemotron 모델 시리즈는 엄청난 잠재력을 보여주었습니다.
기술의 지속적인 발전으로, 수학적 추론을 위한 AI의 새로운 시대가 도래했다고 믿을 만한 이유가 생겼습니다!
'AI > 뉴스' 카테고리의 다른 글
| 2025년 4월 30일 AI 뉴스 (0) | 2025.04.30 |
|---|---|
| SKT 유심 재고 문제의 배경 설명(유심 포맷) (0) | 2025.04.29 |
| 메타, 2025년 10월 차세대 스마트 안경 출시 예정 (1) | 2025.04.28 |
| 2025년 최고의 데이터 보안 플랫폼 (0) | 2025.04.27 |
| 2025년 4월 27일 AI 뉴스 (0) | 2025.04.27 |



